刷算法(10)-搜寻名人

277. 搜寻名人(会员题)

假设你是一个专业的狗仔，参加了一个n人派对，其中每个人被从0到n-1 标号。在这个派对人群当中可能存在一位 “名人”。所谓 “名人” 的定义是：其他所有n-1个人都认识他/她，而他/她并不认识其他任何人。

现在你想要确认这个“名人”是谁，或者确定这里没有“名人”。而你唯一能做的就是问诸如“A 你好呀，请问你认不认识 B呀？”的问题，以确定A是否认识 B。你需要在（渐近意义上）尽可能少的问题内来确定这位 “名人”是谁（或者确定这里没有“名人”）。在本题中，你可以使用辅助函数bool knows(a, b)获取到 A 是否认识 B。请你来实现一个函数int findCelebrity(n)。

派对最多只会有一个 “名人” 参加。若 “名人” 存在，请返回他/她的编号；若 “名人” 不存在，请返回 -1。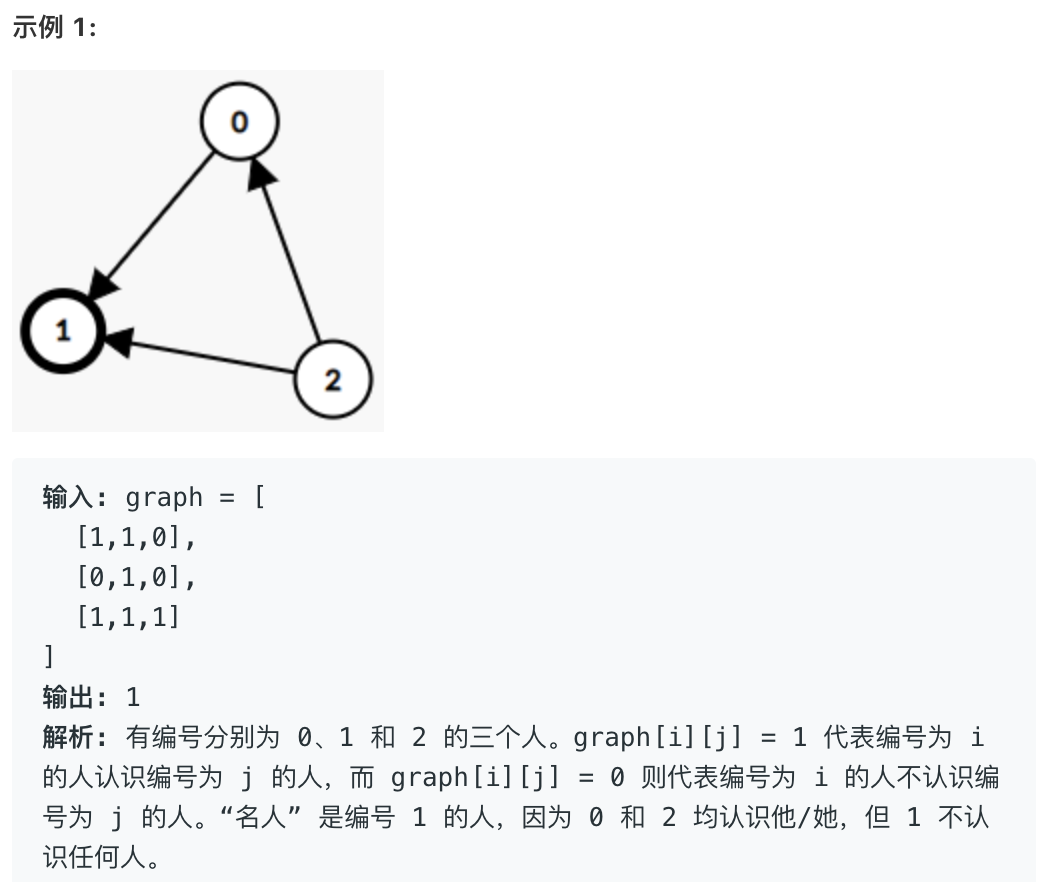

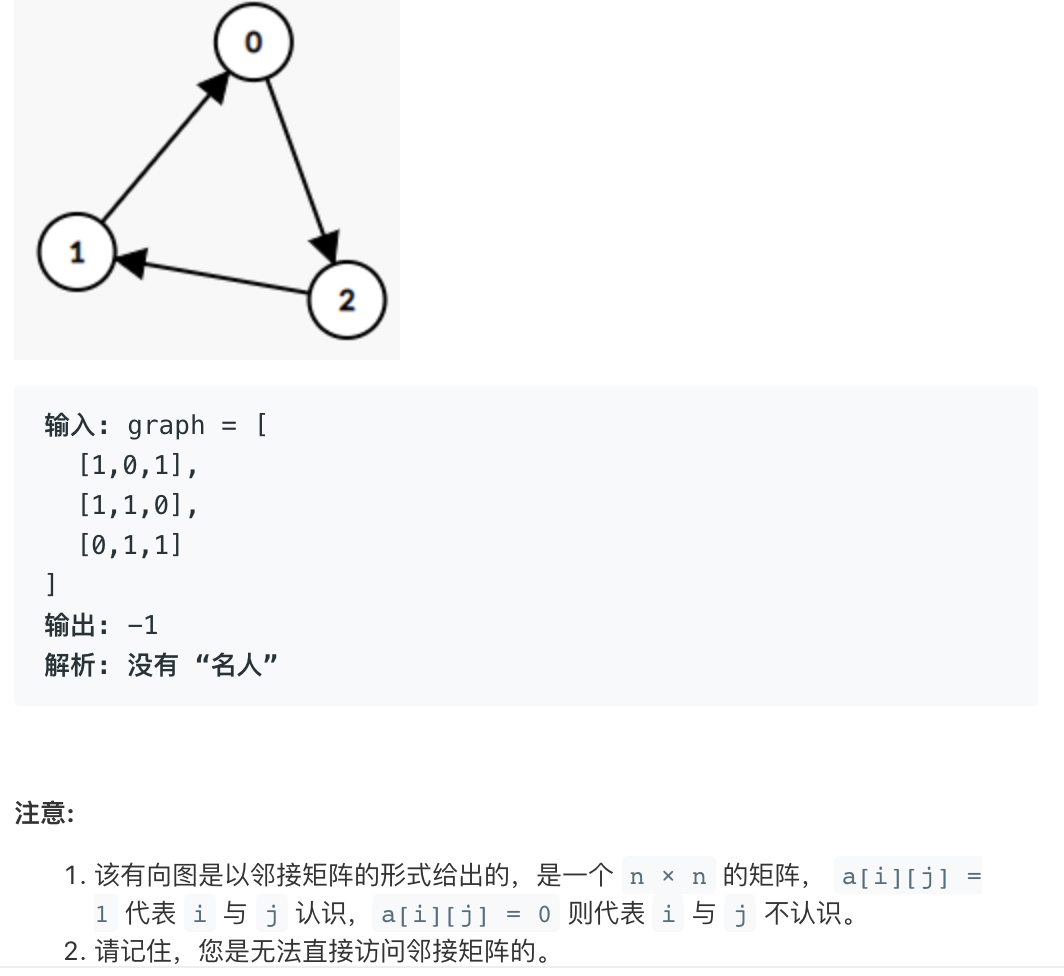
解法1（暴力破解）

从0到n-1，假设其中一个数是名人，然后判断是否满足以下两个条件：

1. 别人都认识他；
2. 他除自己外不认识别人
   代码如下：

   public class Solution extends Relation {
       public int findCelebrity(int n) {
           int result = -1;
           boolean isFail = false;
           for (int mingren = 0; mingren < n; mingren++){
               int others = 0, count = 0;
               while (mingren == others || (knows(others, mingren) && !knows(mingren, others) && others < n){
               count++;
                   // 包括自己名人有n个认识
                   if (count == n){
                       return mingren;
                   }
               others++;
               }
           }
           return result;
       }
   }

注意这里假设mingren后，找其他人的时候一定是从头也就是0开始找，不存在从mingren + 1开始找这个说法。上述算法耗时11ms。

贪心算法（优化后）

先假设第一个数就是名人，然后如果他认识别人，那就当其他人是名人。如果存在名人，则这个mingren只满足中间交换时i之后的人他不认识，而i之前的还要再确保一下。所以出了循环后针对修正后的名人，看看是不是满足条件。代码如下：

public class Solution extends Relation {
    public int findCelebrity(int n) {
        int mingren = 0;
        for (int i = 1; i < n; i++){
            if (knows(mingren, i)){
                mingren = i;
            }
        }
        
        for (int j = 0; j<n; j++){
            if (j != mingren && (knows(mingren, j) || !knows(j, mingren))){
                return -1;
            }
        }
        return mingren;
        
    }
}

优化后耗时8ms。

参考

• 暴力法
• 官方解法